概率值（probability value）

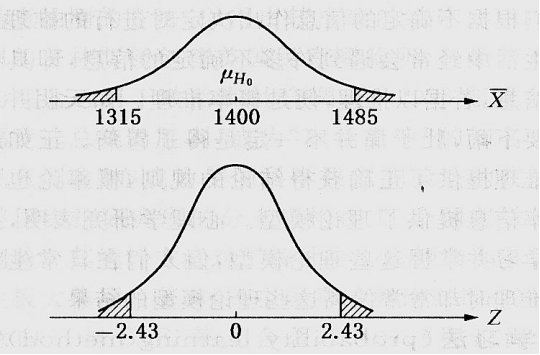
一译“概值”、“P值”。假设检验术语。分单侧概率值与双侧概率值两类。（1）单侧概率值，又分右侧概率值和左侧概率值。对于任何要检验的零假设\(H_0\)，\(H_0\)的右侧概率值是指“若\(H_0\)为真，样本统计量大于或等于实际观测值”的概率，\(H_0\)的左侧概率值是指“若\(H_0\)为真，样本统计量小于或等于实际观测值”的概率，两者均可写成\(P_r\)。如某总体\(X\sim N(\mu,\sigma^2)\)，其中\(\sigma^2=(350)^2\)，而\(\mu\)未知。现欲检验的假设是\(H_0:\mu=1400\)；\(H_1:\mu>1400\)。这属于右侧检验问题。现随机抽取\(n=100\)的样本，算得样本算术平均数\(\bar{X}=1485\)。检验统计量是\(Z=\frac{\bar{X}-1400}{\sigma/\sqrt{n}}=\frac{\bar{X}-1400}{350/\sqrt{100}}=\frac{\bar{X}-1400}{35}\)，在\(H_0\)成立的条件下，\(Z\)服从标准正态分布。在\(\bar{X}=1485\)时，\(Z=\frac{1485-1400}{35}=2.43\)。可查表得\(P_r(Z\ge2.43)=P_r(\bar{X}\ge1485)=0.0075\)。这就是检验\(H_0\)的概率值。它说明“\(Z\ge2.43\)”或“\(\bar{X}\ge 1485\)”的概率只有\(0.0075\)，这是很小的可能性。若\(H_0\)是对的，\(\bar{X}\)要大于或等于\(1485\)是非常困难的。然而现在\(\bar{X}=1485\)，这个事实与\(H_0\)是严重不符的，可以拒绝\(H_0\)。（2）双侧概率值，指“若\(H_0\)真，统计量向双尾偏离至少到观测值之外”的概率，用\(P_r\)表示。上例中，若假设是\(H_0:\mu=1400\)；\(H_1:\mu>1400\)，由于Z分布的对称性，有\(P_r(Z\ge2.43)=P_r(Z\le -2.43)=0.0075\)。于是概率值等于\(P_r(|Z|\ge2.43)=0.0075+0.0075=0.015\)。下面是由统计量\(\bar{X}\)和\(Z\)的分布表示的概率值。