验证性因素分析（confirmatory factor analysis）

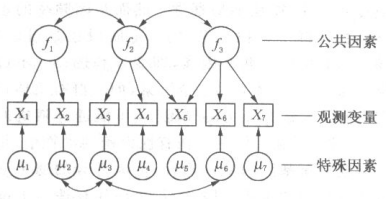
一译“实证性因素分析”。因素分析的一种。与“探索性因素分析”相对。强调验证理论分析结果的可靠性。20世纪60年代以来因素分析的主要进展。研究者首先根据已有的专业知识和实践经验决定：（1）各个观测变量分别受哪些公共因素影响；（2）哪几对公共因素之间是相关的；（3）哪几对特殊因素之间是相关的。下图是研究者根据经验提出的分析模型路径图。图中的双向箭头表示两者相关。有时研究者会同时提出几种不同的假设模型。可通过多种方法检验假设模型而作出最后的选择，并估计出未知参数。其数学模型为\(X=Af+\mu\)，其中\(X={(X_1,X_2,\cdots,X_p)}'\)是标准化观测变量向量，\(f={(f_1,f_2,\cdots,f_m)}'\)是公共因素向量，满足\(E(f)=0\)，\(A=(a_{ik})_{p\times m}\)是因素负荷矩阵，\(\mu={(\mu_1,\mu_2,\cdots,\mu_p)}'\)是特殊因素向量。满足\(E(\mu)=0\)，\(m<p\)。由此可导出观测变量协方差矩阵\(Cov(X)=\Sigma=A\Phi {A}'+\Theta\)，其中\(\Phi=E(f{f}')\)，\(\Theta=E(\mu {\mu}')\)，\(A\)为因素负荷矩阵。研究者就是根据专业经验对\(A\)、\(\Phi\)、\(\Theta\)的某些参数加以指定或约束，然后用极大似然法等估计矩阵\(A\)、\(\Phi\)、\(\Theta\)中的未知参数。其最大优点是数学模型的灵活性。模型的灵活性使它能有效地应用于心理和教育研究的许多实际问题。验证性因素模型是结构方程式模型的一种很特殊的子模型。用于分析结构方程式模型的常用软件是；LISREL、AMOS和EQS。利用这些软件可作验证性因素分析。