分位数（fractiles）

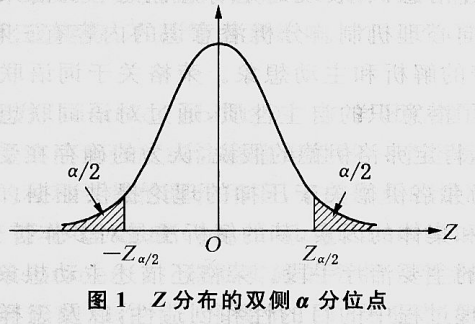
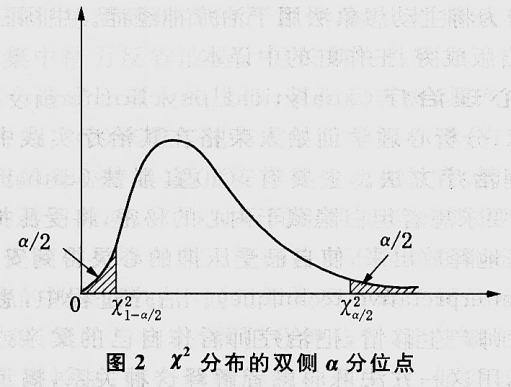
描述统计量的一种。将一组数据由小至大排列，若数列中的数据\(X_\alpha\)满足数列中小于或等于\(X_\alpha\)的数据个数所占比例是\(\alpha\)这一条件，则称α为该数据组的“α分位数”或“α分位点”。这里的α满足0<α<1。根据所占比例α的不同，可分为四分位数、十分位数、0.5分位数、百分位数等。在推断统计中（如区间估计、假设检验等），也常提到分位数的概念，但其含义应当按照编制的统计量分布数值表的规定去理解。如标准正态分布中的“双侧α分位点”，是指满足\(P_r(Z>Z_{\alpha/2})=P_r(Z<-Z_{\alpha/2})=\frac{\alpha}{2}\)公式的两个点\(Z_{\alpha/2}\)与\(-Z_{\alpha/2}\)，这里\(Z\)是服从标准正态分布的变量（如图1）。自由度为\(n\)的\(\chi ^2\)统计量的分布中的“双侧α分位点”\(\chi _{1-\alpha/2}^2\)与\(\chi _{\alpha/2}^2\)（如图2）。