因素负荷（factor loading）

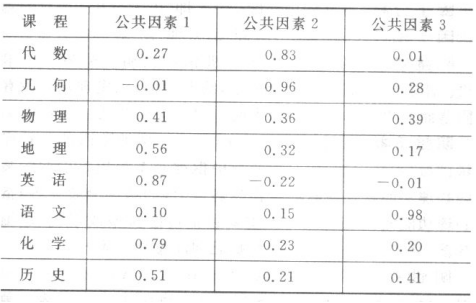
因素分析术语。因素模型中公共因素的系数。设\(Z_i=a_{i1}f_1+a_{i2}f2+\cdots+a_{im}f_m+d_{i\mu i}, \ i=1,\cdots,p\)，式中\(f_1,\cdots,f_m\)是公共因素，是只和\(Z_i\)有关的特殊因素，矩阵\(A=\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1m} \\ a_{21} & a_{22} & \cdots & a_{2m} \\ \cdots & \cdots & \cdots & \cdots \\ a_{p1} & a_{p2} & \cdots & a_{pm} \end{bmatrix}\)称为因素负荷矩阵。在正交因素模型中，变量\(Z_i\)在第\(j\)个因素\(f_j\)上的负荷就是\(Z_i\)与\(f_i\)的相关系数。因素负荷是识别公共因素的依据，在同一个公共因素上有较大负荷的变量作为一组，它们的综合属性将用来解释这个公共因素。若因素负荷矩阵作了旋转，则要用旋转后的负荷矩阵来解释因素。如若对学生8门课程的测验成绩所做的因素分析有3个公共因素，负荷矩阵如表。

根据负荷矩阵可对公共因素作出解释。公共因素1主要由英语和化学表征，地理和历史对其也有较大的依赖性，可将该因素解释为识记方面的能力。公共因素2主要由代数和几何表征，可解释为抽象思维和逻辑推理能力。公共因素3主要由语文表征，历史对其也有较大的依赖性，可解释为语言和文字表达能力。