控制阶（control order）

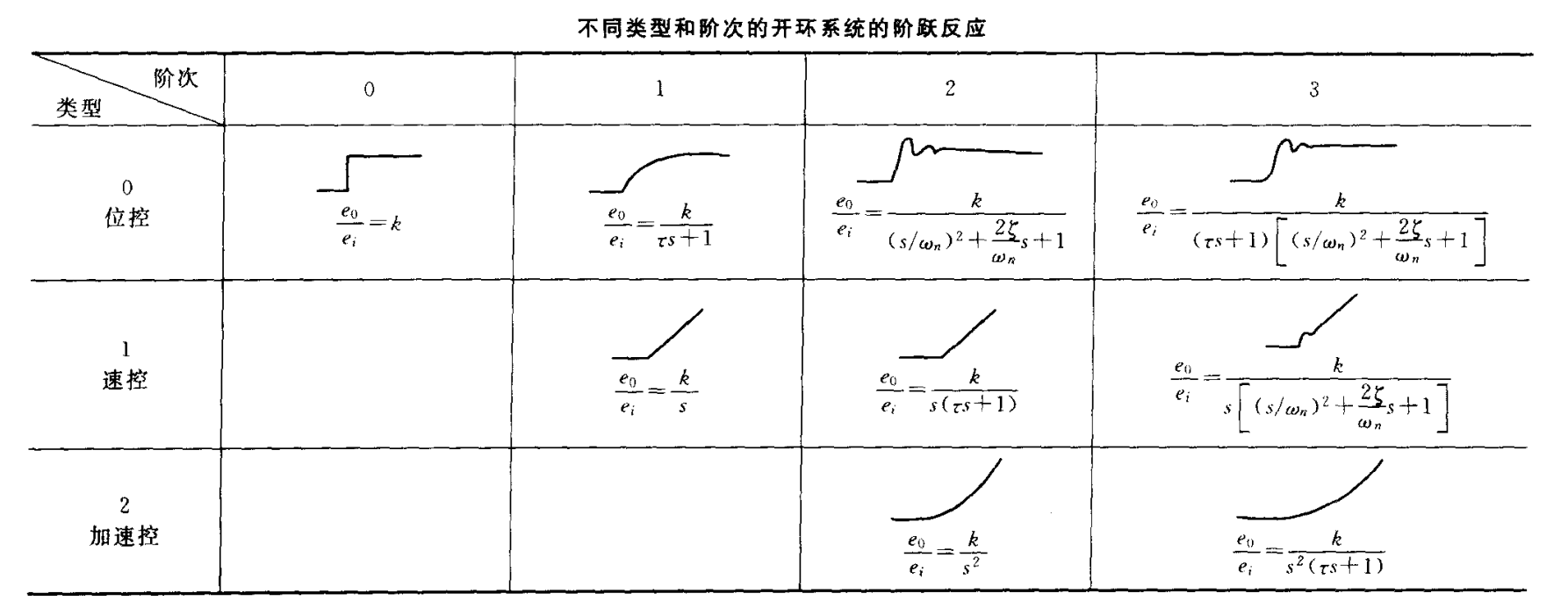
描述系统的输入与输出关系微分方程中含有的导数的最高阶次。对于一个单输入-单输出的线性定常系统，它的输入与输出满足的关系可用微分方程表示为\(a_{n}y^{(n)}+a_{n-1}y^{(n-1)}+\cdots +a_1y^'+a_0y=b_mx^{(m)}+b_{m-1}x^{(m-1)}+\cdots+b_1x^'+b_0x\)。式中的\(a_0 \cdots a_n,b_0 \cdots b_m\)均为常数，\(n\)、\(m\)为正整数，\(n \ge m\)。用上述微分方程描述的系统称为\(n\)阶系统。对于线性定常系统的动力特性可用它的传递函数来描述。以上系统的传递函数表示为\(G(s)=(b_m s^m+b_{m-1}s^{m-1}+\cdots +b_1s+b_0)/(a_ns^n+a_{n-1}s^{n-1}+\cdots +a_1s+a_0)\)。由于传递函数分母中\(s\)的最高幂等于相应的微分方程中\(y\)的导数的最高阶次，因此控制阶也可定义为传递函数分母中出现的\(s\)的最高幂。根据传递函数的分母所能提出的\(s\)公因子的幂可划分出不同的系统控制反应类型（即控制类型）。若一个系统的传递函数是\(G(s)=(b_m s^m+b_{m-1}s^{m-1}+\cdots +b_1s+b_0)/[s^k(a_ns^j+a_{n-1}s^{j-1}+\cdots +a_{k+1}s+a_k)]\)，这样的系统称为\(k\)型\(k+j\)阶系统。当\(k\)等于0、1和2时系统又分别可称为位移控制型、速度控制型和加速度控制型。下表表明不同类型和阶次的开环系统的阶跃反应图解。关于控制阶的工程心理学研究主要涉及纯控制阶（即\(k\)、\(k/s\)、\(k/s^2\)等）的效应。纯控制阶与控制类型是一致的，纯控制阶效应与系统输入有关。对于随机输入，操作员对位置和速度都要加以控制，用零阶和一阶控制各有利弊，它们的绩效基本相等。在二阶或二阶以上的高阶追踪中，人需要觉察高阶导数，进行积分计算，并要预测误差，一般较难适应。