一个正态总体方差的置信区间（confidence interval for variance of a normal distribution）

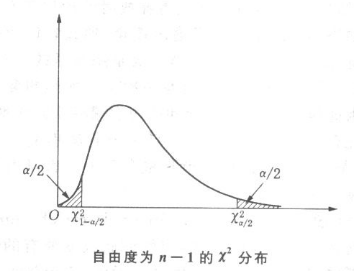
区间估计置信区间的一种。设总体\(X \sim N(\mu,\sigma^2)\)，为了给出未知方差\(\sigma^2\)的估计区间，对\(X\)进行\(n\)次观测获得随机样本\(X_1,X_2,\cdots,X_n\)。由统计理论知道统计量\(\chi^2=\frac{(n-1)S^2}{\sigma^2}\)服从自由度为\(n-1\)的卡方分布（式中\(S^2=\frac{1}{n-1}\sum\limits_{i=1}^{n}(X_i-\bar{X})^2\)）。然后由下面等式\(P \left \{ \chi_{1-\alpha/2}^2 \le \frac{(n-1)S^2}{\sigma^2} \le \chi_{\alpha/2}^2 \right \}=1-\alpha\)可得到总体方差\(\sigma^2\)的置信度为（\(1-\alpha\)）的估计区间为\(\frac{(n-1)S^2}{\chi_{\alpha/s}^2} \le \sigma^2 \le \frac{(n-1)S^2}{\chi_{1-\alpha/s}^2}\)。上面\(\chi_{\alpha/2}^2\)是卡方分布的上侧\(\alpha/2\)分位点，\(\chi_{1-\alpha/2}^2\)是下侧\(1-\alpha/2\)分位点（如图所示）。